什么是堆?
堆是一种满足以下条件的树:
堆中的每一个节点值都大于等于(或小于等于)子树中所有节点的值。或者说,任意一个节点的值都大于等于(或小于等于)所有子节点的值。
大家可以把堆(最大堆)理解为一个公司,这个公司很公平,谁能力强谁就当老大,不存在弱的人当老大,老大手底下的人一定不会比他强。这样有助于理解后续堆的操作。
!!!特别提示:
- 很多博客说堆是完全二叉树,其实并非如此,堆不一定是完全二叉树,只是为了方便存储和索引,我们通常用完全二叉树的形式来表示堆,事实上,广为人知的斐波那契堆和二项堆就不是完全二叉树,它们甚至都不是二叉树。
- (二叉)堆是一个数组,它可以被看成是一个 近似的完全二叉树。——《算法导论》第三版
大家可以尝试判断下面给出的图是否是二叉树?
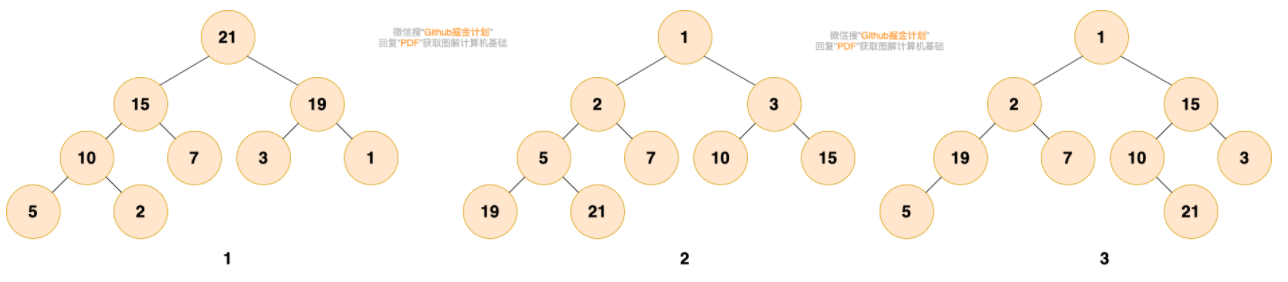
第1个和第2个是堆。第1个是最大堆,每个节点都比子树中所有节点大。第2个是最小堆,每个节点都比子树中所有节点小。
第3个不是,第三个中,根结点1比2和15小,而15却比3大,19比5大,不满足堆的性质。
堆的用途
当我们只关心所有数据中的最大值或者最小值,存在多次获取最大值或者最小值,多次插入或删除数据时,就可以使用堆。
有小伙伴可能会想到用有序数组,初始化一个有序数组时间复杂度是 O(nlog(n)),查找最大值或者最小值时间复杂度都是 O(1),但是,涉及到更新(插入或删除)数据时,时间复杂度为 O(n),即使是使用复杂度为 O(log(n)) 的二分法找到要插入或者删除的数据,在移动数据时也需要 O(n) 的时间复杂度。
相对于有序数组而言,堆的主要优势在于更新数据效率较高。 堆的初始化时间复杂度为 O(nlog(n)),堆可以做到O(1)时间复杂度取出最大值或者最小值,O(log(n))时间复杂度插入或者删除数据,具体操作在后续章节详细介绍。
堆的分类
堆分为 最大堆 和 最小堆。二者的区别在于节点的排序方式。
- 最大堆 :堆中的每一个节点的值都大于等于子树中所有节点的值
- 最小堆:堆中的每一个节点的值都小于等于子树中所有节点的值
如下图所示,图1是最大堆,图2是最小堆
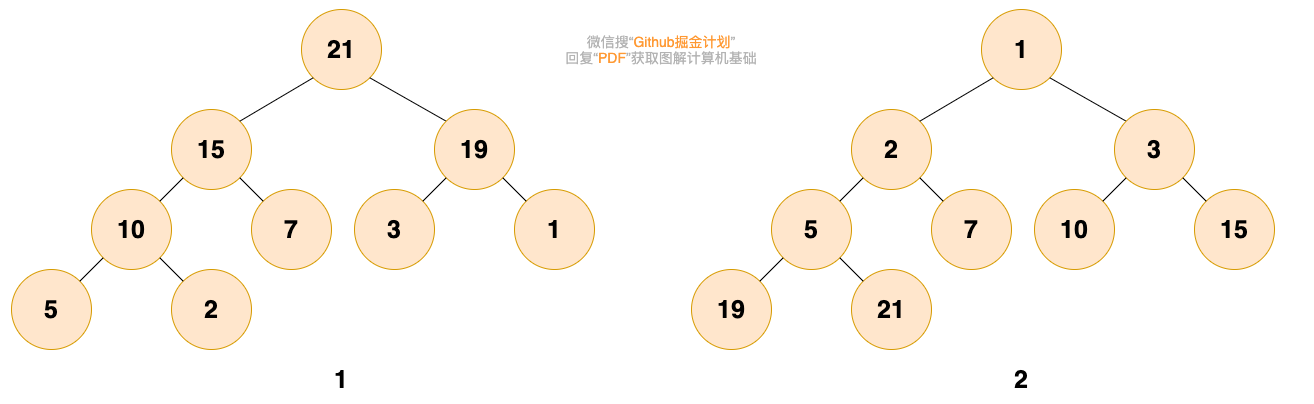
堆的存储
之前介绍树的时候说过,由于完全二叉树的优秀性质,利用数组存储二叉树即节省空间,又方便索引(若根结点的序号为1,那么对于树中任意节点i,其左子节点序号为 2*i,右子节点序号为 2*i+1)。
为了方便存储和索引,(二叉)堆可以用完全二叉树的形式进行存储。存储的方式如下图所示:
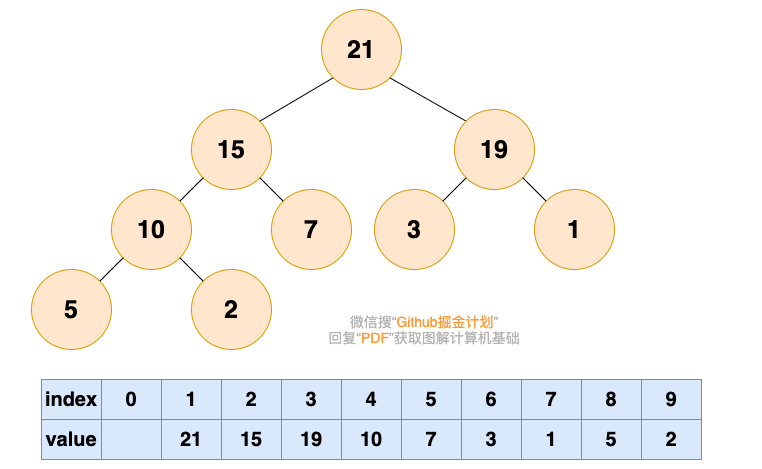
堆的操作
堆的更新操作主要包括两种 : 插入元素 和 删除堆顶元素。操作过程需要着重掌握和理解。
在进入正题之前,再重申一遍,堆是一个公平的公司,有能力的人自然会走到与他能力所匹配的位置
插入元素
插入元素,作为一个新入职的员工,初来乍到,这个员工需要从基层做起
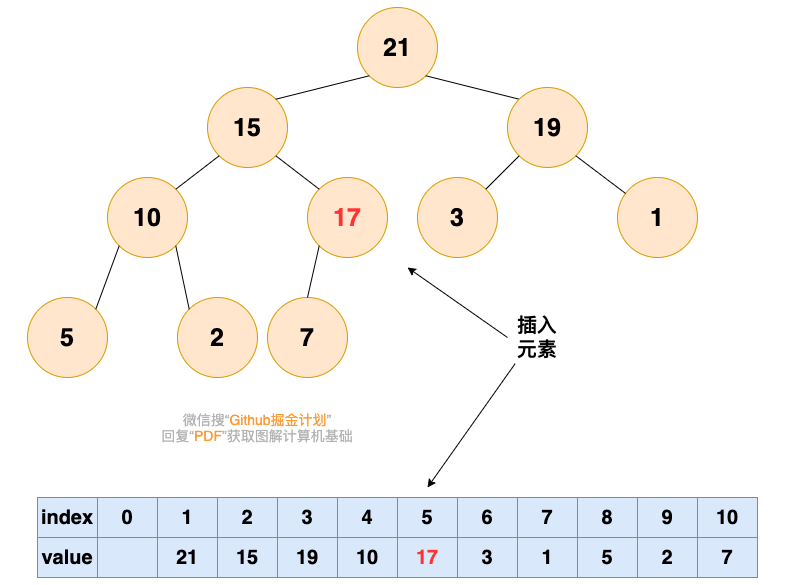
- 将要插入的元素放到最后
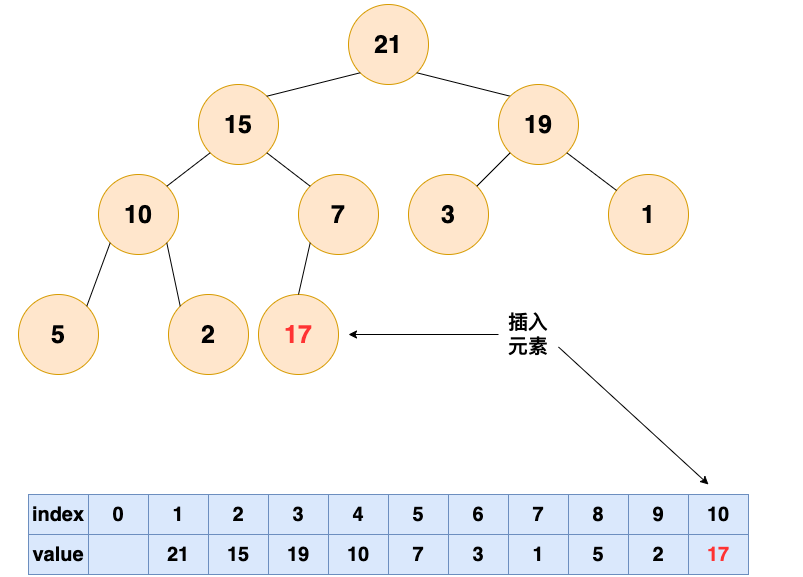
有能力的人会逐渐升职加薪,是金子总会发光的!!!
- 从底向上,如果父结点比该元素大,则该节点和父结点交换,直到无法交换
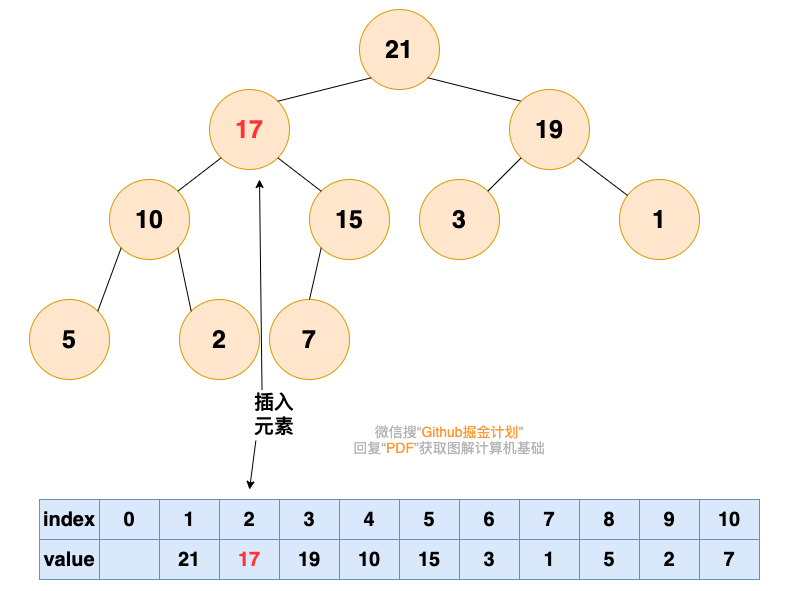
删除堆顶元素
根据堆的性质可知,最大堆的堆顶元素为所有元素中最大的,最小堆的堆顶元素是所有元素中最小的。当我们需要多次查找最大元素或者最小元素的时候,可以利用堆来实现。
删除堆顶元素后,为了保持堆的性质,需要对堆的结构进行调整,我们将这个过程称之为”堆化“,堆化的方法分为两种:
- 一种是自底向上的堆化,上述的插入元素所使用的就是自底向上的堆化,元素从最底部向上移动。
- 另一种是自顶向下堆化,元素由最顶部向下移动。在讲解删除堆顶元素的方法时,我将阐述这两种操作的过程,大家可以体会一下二者的不同。
自底向上堆化
在堆这个公司中,会出现老大离职的现象,老大离职之后,他的位置就空出来了
首先删除堆顶元素,使得数组中下标为1的位置空出。
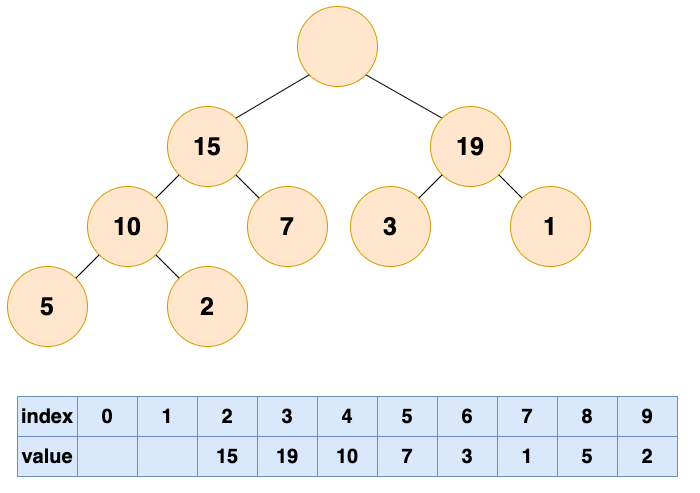
那么他的位置由谁来接替呢,当然是他的直接下属了,谁能力强就让谁上呗
比较根结点的左子节点和右子节点,也就是下标为2,3的数组元素,将较大的元素填充到根结点(下标为1)的位置。
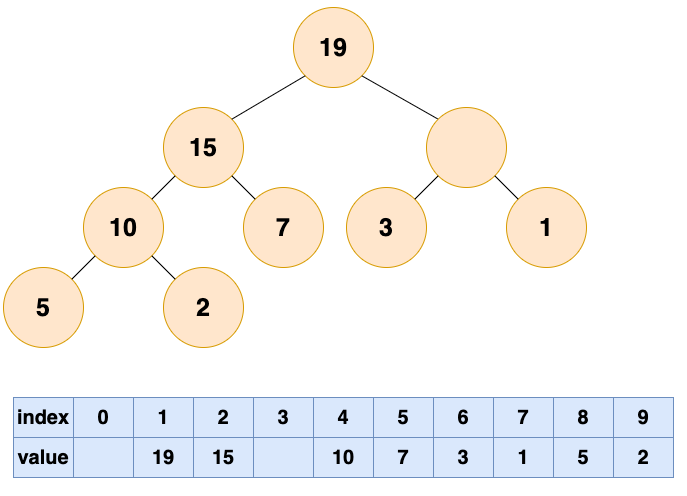
这个时候又空出一个位置了,老规矩,谁有能力谁上
一直循环比较空出位置的左右子节点,并将较大者移至空位,直到堆的最底部
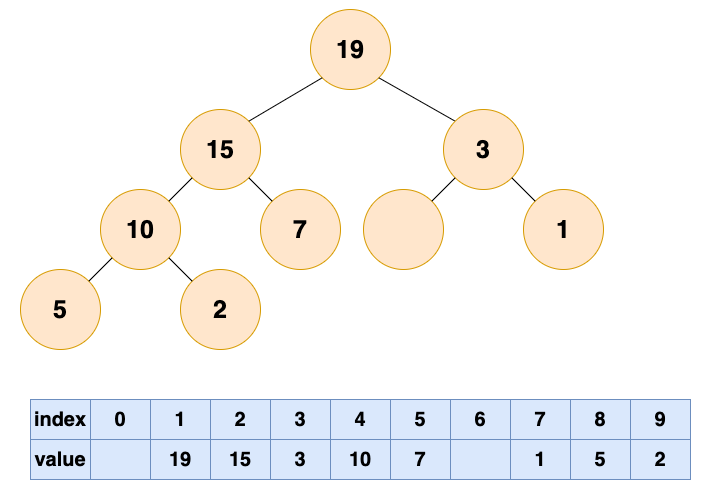
这个时候已经完成了自底向上的堆化,没有元素可以填补空缺了,但是,我们可以看到数组中出现了“气泡”,这会导致存储空间的浪费。接下来我们试试自顶向下堆化。
自顶向下堆化
自顶向下的堆化用一个词形容就是“石沉大海”,那么第一件事情,就是把石头抬起来,从海面扔下去。这个石头就是堆的最后一个元素,我们将最后一个元素移动到堆顶。
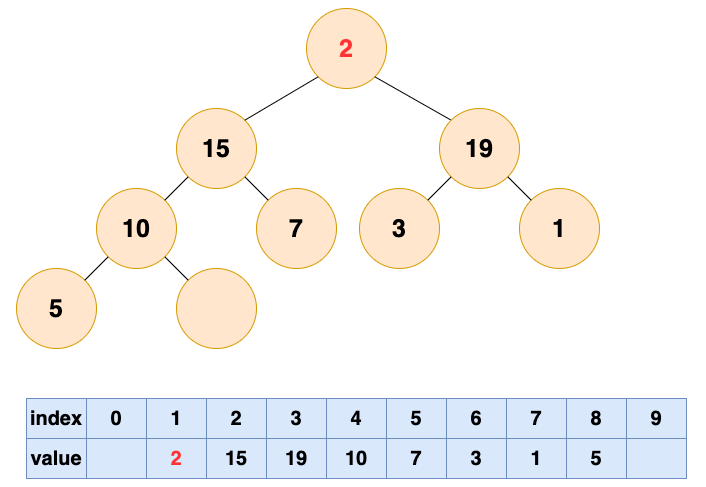
然后开始将这个石头沉入海底,不停与左右子节点的值进行比较,和较大的子节点交换位置,直到无法交换位置。
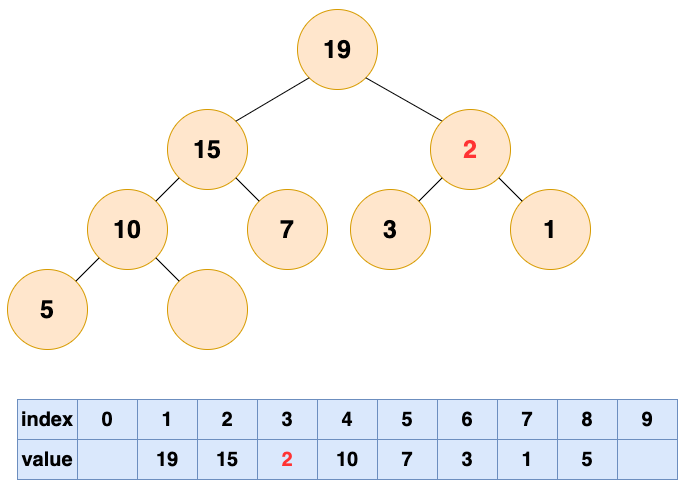
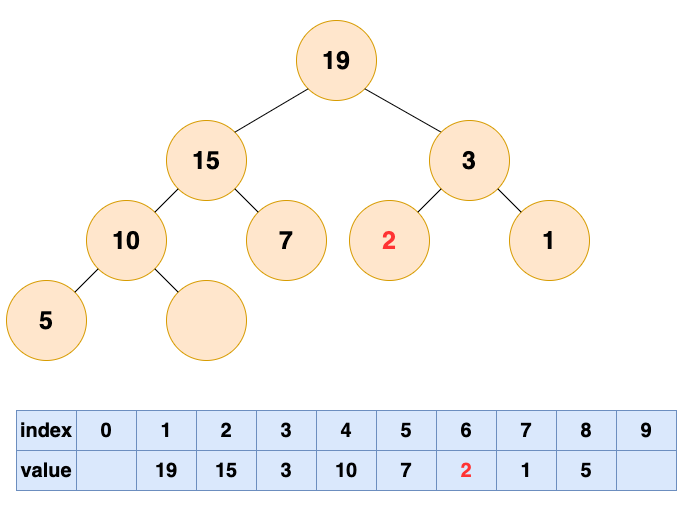
堆的操作总结
- 插入元素 :先将元素放至数组末尾,再自底向上堆化,将末尾元素上浮
- 删除堆顶元素 :删除堆顶元素,将末尾元素放至堆顶,再自顶向下堆化,将堆顶元素下沉。也可以自底向上堆化,只是会产生“气泡”,浪费存储空间。最好采用自顶向下堆化的方式。
堆排序
堆排序的过程分为两步:
- 第一步是建堆,将一个无序的数组建立为一个堆
- 第二步是排序,将堆顶元素取出,然后对剩下的元素进行堆化,反复迭代,直到所有元素被取出为止。
建堆
如果你已经足够了解堆化的过程,那么建堆的过程掌握起来就比较容易了。建堆的过程就是一个对所有非叶节点的自顶向下堆化过程。
首先要了解哪些是非叶节点,最后一个节点的父结点及它之前的元素,都是非叶节点。也就是说,如果节点个数为n,那么我们需要对n/2到1的节点进行自顶向下(沉底)堆化。
具体过程如下图:
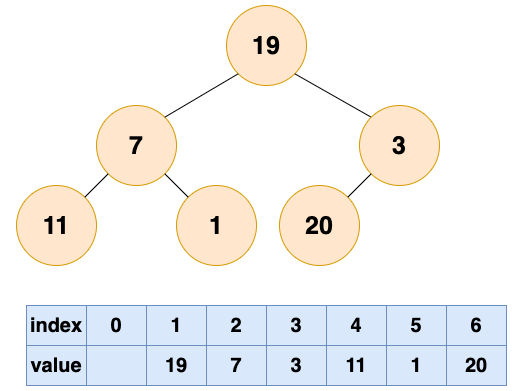
将初始的无序数组抽象为一棵树,图中的节点个数为6,所以4,5,6节点为叶节点,1,2,3节点为非叶节点,所以要对1-3号节点进行自顶向下(沉底)堆化,注意,顺序是从后往前堆化,从3号节点开始,一直到1号节点。 3号节点堆化结果:
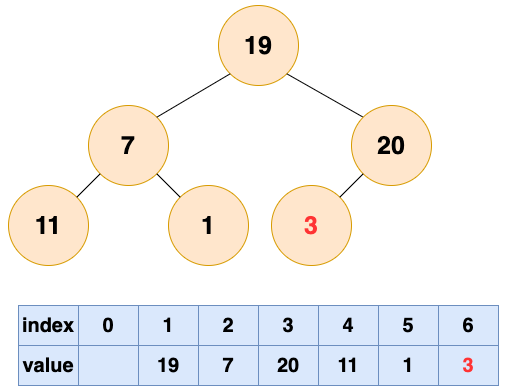
2号节点堆化结果:
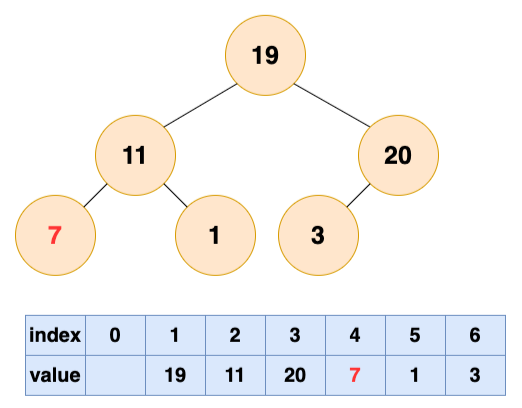
1号节点堆化结果:
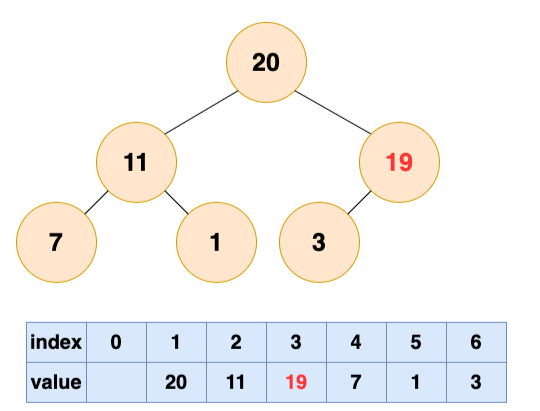
至此,数组所对应的树已经成为了一个最大堆,建堆完成!
排序
由于堆顶元素是所有元素中最大的,所以我们重复取出堆顶元素,将这个最大的堆顶元素放至数组末尾,并对剩下的元素进行堆化即可。
现在思考两个问题:
- 删除堆顶元素后需要执行自顶向下(沉底)堆化还是自底向上(上浮)堆化?
- 取出的堆顶元素存在哪,新建一个数组存?
先回答第一个问题,我们需要执行自顶向下(沉底)堆化,这个堆化一开始要将末尾元素移动至堆顶,这个时候末尾的位置就空出来了,由于堆中元素已经减小,这个位置不会再被使用,所以我们可以将取出的元素放在末尾。
机智的小伙伴已经发现了,这其实是做了一次交换操作,将堆顶和末尾元素调换位置,从而将取出堆顶元素和堆化的第一步(将末尾元素放至根结点位置)进行合并。
详细过程如下图所示:
取出第一个元素并堆化:
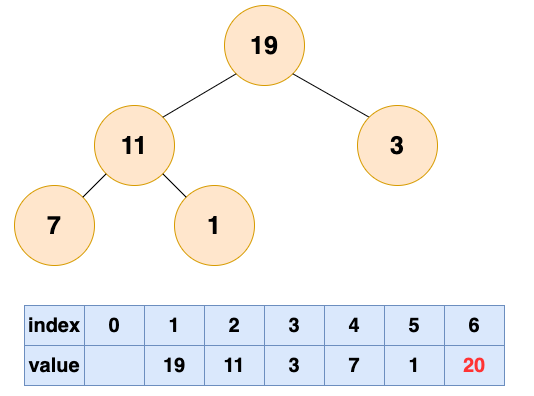
取出第二个元素并堆化:
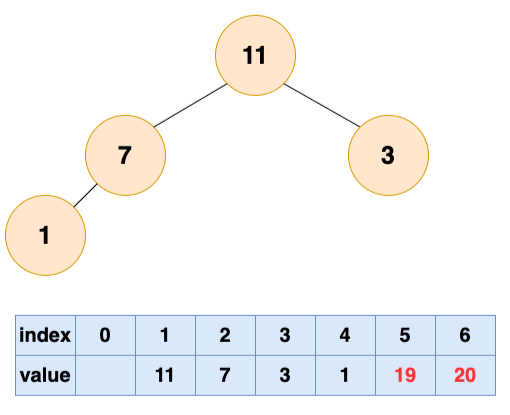
取出第三个元素并堆化:
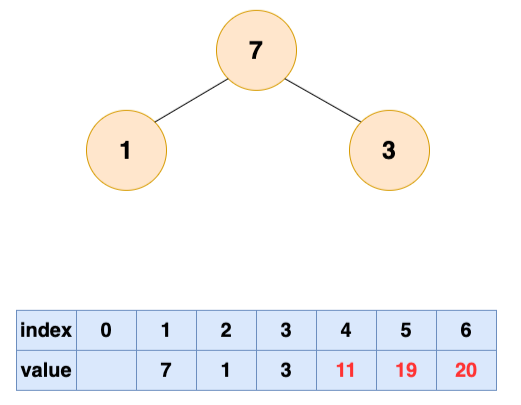
取出第四个元素并堆化:
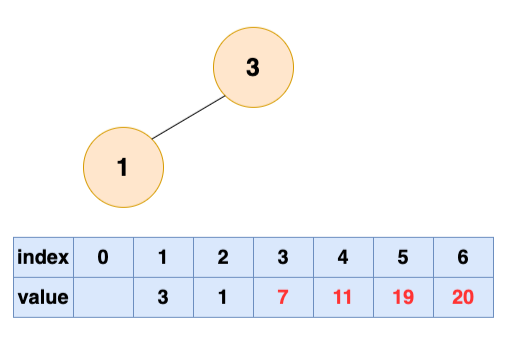
取出第五个元素并堆化:
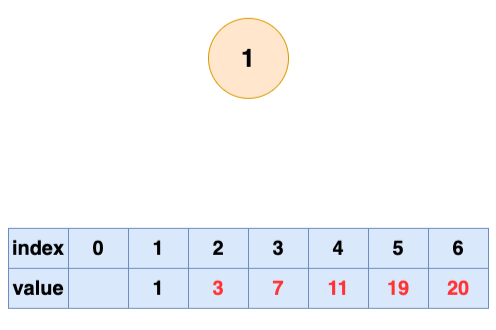
取出第六个元素并堆化:
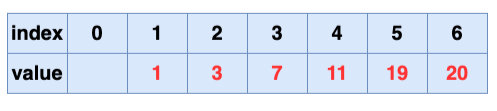
堆排序完成!








