优先队列和堆

Marlowe

发布于：Jun 1, 2021

2.8k words

10 min

什么是优先队列？

听这个名字就能知道，优先队列也是一种队列，只不过不同的是，优先队列的出队顺序是按照优先级来的；在有些情况下，可能需要找到元素集合中的最小或者最大元素，可以利用优先队列ADT来完成操作，优先队列ADT是一种数据结构，它支持插入和删除最小值操作（返回并删除最小元素）或删除最大值操作（返回并删除最大元素）；

这些操作等价于队列的enQueue和deQueue操作，区别在于，对于优先队列，元素进入队列的顺序可能与其被操作的顺序不同，作业调度是优先队列的一个应用实例，它根据优先级的高低而不是先到先服务的方式来进行调度；

如果最小键值元素拥有最高的优先级，那么这种优先队列叫作升序优先队列（即总是先删除最小的元素），类似的，如果最大键值元素拥有最高的优先级，那么这种优先队列叫作降序优先队列（即总是先删除最大的元素）；由于这两种类型时对称的，所以只需要关注其中一种，如升序优先队列；

优先队列ADT

下面操作组成了优先队列的一个ADT；

1.优先队列的主要操作 优先队列是元素的容器，每个元素有一个相关的键值；

insert(key, data)：插入键值为key的数据到优先队列中，元素以其key进行排序；
deleteMin/deleteMax：删除并返回最小/最大键值的元素；
getMinimum/getMaximum：返回最小/最大剑指的元素，但不删除它；

2.优先队列的辅助操作

第k最小/第k最大：返回优先队列中键值为第k个最小/最大的元素；
大小（size）：返回优先队列中的元素个数；
堆排序（Heap Sort）：基于键值的优先级将优先队列中的元素进行排序；

优先队列的应用

数据压缩：赫夫曼编码算法；
最短路径算法：Dijkstra算法；
最小生成树算法：Prim算法；
事件驱动仿真：顾客排队算法；
选择问题：查找第k个最小元素；
等等等等….

堆和二叉堆

什么是堆

堆是一颗具有特定性质的二叉树，堆的基本要求就是堆中所有结点的值必须大于或等于（或小于或等于）其孩子结点的值，这也称为堆的性质；堆还有另一个性质，就是当 h > 0 时，所有叶子结点都处于第 h 或 h - 1 层（其中 h 为树的高度，完全二叉树），也就是说，堆应该是一颗完全二叉树；

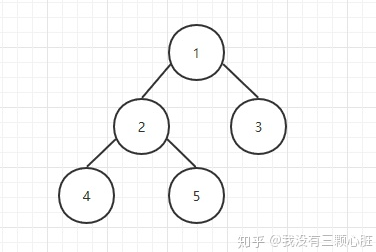
在下面的例子中，左边的树为堆（每个元素都大于其孩子结点的值），而右边的树不是堆（因为5大于其孩子结点2）

二叉堆

在二叉堆中，每个结点最多有两个孩子结点，在实际应用中，二叉堆已经足够满足需求，因此接下来主要讨论二叉最小堆和二叉最大堆；

堆的表示：在描述堆的操作前，首先来看堆是怎样表示的，一种可能的方法就是使用数组，因为堆在形式上是一颗完全二叉树，用数组来存储它不会浪费任何空间，例如下图：

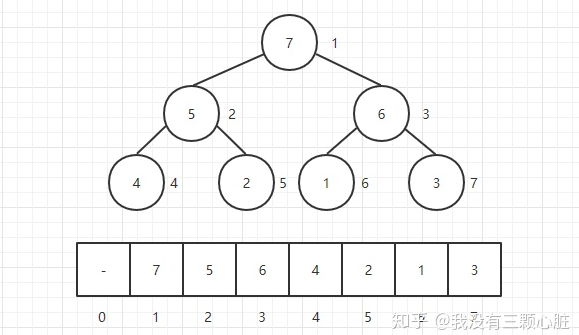
用数组来表示堆不仅不会浪费空间还具有一定的优势：

每个结点的左孩子为下标i的2倍：left child(i) = i * 2；每个结点的右孩子为下标i的2倍加1：right child(i) = i * 2 + 1
每个结点的父亲结点为下标的二分之一：parent(i) = i / 2，注意这里是整数除，2和3除以2都为1，大家可以验证一下；
注意：这里是把下标为0的地方空出来了的，主要是为了方便理解，如果0不空出来只需要在计算的时候把i值往右偏移一个位置就行了（也就是加1，大家可以试试，下面的演示也采取这样的方式）；

二叉堆的相关操作

堆的基本结构

public class MaxHeap<E extends Comparable<E>> {
    private Array<E> data;
    public MaxHeap(int capacity){ data = new Array<>(capacity); }
    public MaxHeap(){ data = new Array<>(); }
    // 返回堆中的元素个数    public int size(){ return data.getSize(); }
    // 返回一个布尔值, 表示堆中是否为空    public boolean isEmpty(){ return data.isEmpty(); }
    // 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引    private int parent(int index){
        if(index == 0)
            throw new IllegalArgumentException("index-0 doesn't have parent.");
        return (index - 1) / 2;
    }
    // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引    private int leftChild(int index){ return index * 2 + 1; }
    // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引    private int rightChild(int index){ return index * 2 + 2; }
}

向堆中添加元素和Sift Up

当插入一个元素到堆中时，它可能不满足堆的性质，在这种情况下，需要调整堆中元素的位置使之重新变成堆，这个过程称为堆化（heapifying）；在最大堆中，要堆化一个元素，需要找到它的父亲结点，如果不满足堆的基本性质则交换两个元素的位置，重复该过程直到每个结点都满足堆的性质为止，下面我们来模拟一下这个过程：

下面我们在该堆中插入一个新的元素26：

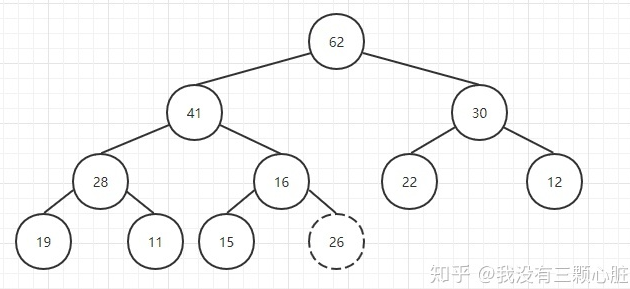
我们通过索引（上面的公式）可以很容易地找到新插入元素的父亲结点，然后比较它们的大小，如果新元素更大则交换两个元素的位置，这个操作就相当于把该元素上浮了一下：

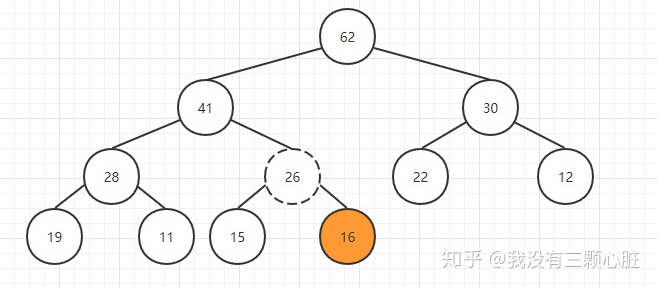
重复该操作直到26到了一个满足堆条件的位置，此时就完成了插入的操作：

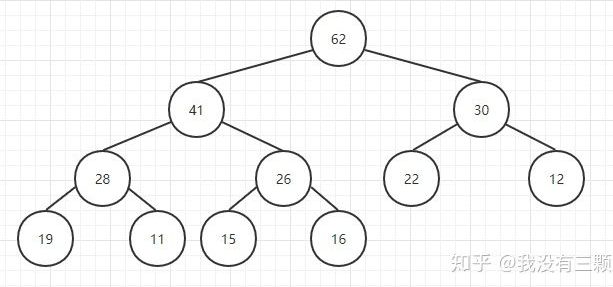
对应的代码如下：

// 向堆中添加元素public void add(E e){
    data.addLast(e);
    siftUp(data.getSize() - 1);
}
private void siftUp(int k){

    while(k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0 ){
        data.swap(k, parent(k));
        k = parent(k);
    }
}

取出堆中的最大元素和Sift Down

如果理解了上述的过程，那么取出堆中的最大元素（堆顶元素）将变得容易，不过这里运用到一个小技巧，就是用最后一个元素替换掉栈顶元素，然后把最后一个元素删除掉，这样一来元素的总个数也满足条件，然后只需要把栈顶元素依次往下调整就好了，这个操作就叫做Sift Down（下沉）：

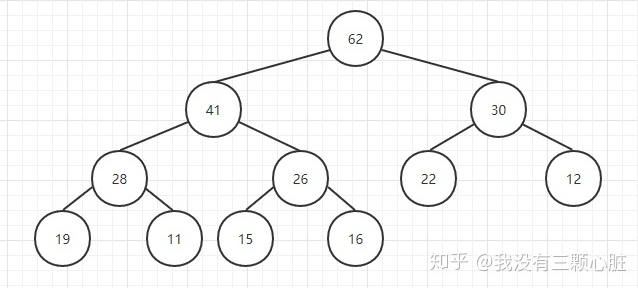
用最后元素替换掉栈顶元素，然后删除最后一个元素：

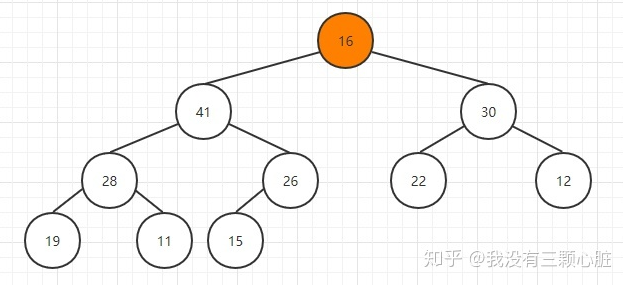
然后比较其孩子结点的大小：

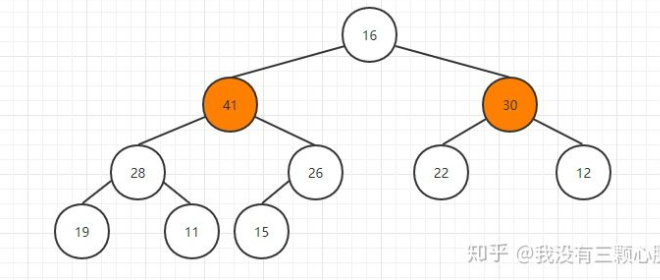
如果不满足堆的条件，那么就跟孩子结点中较大的一个交换位置：

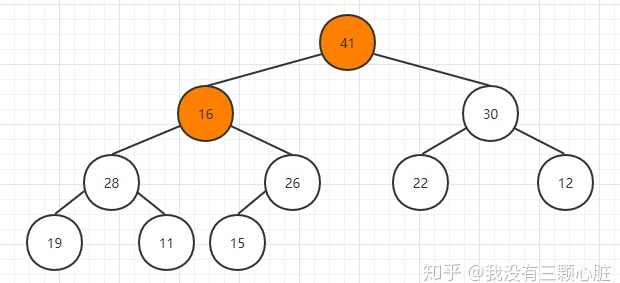
重复该步骤，直到16到达合适的位置：

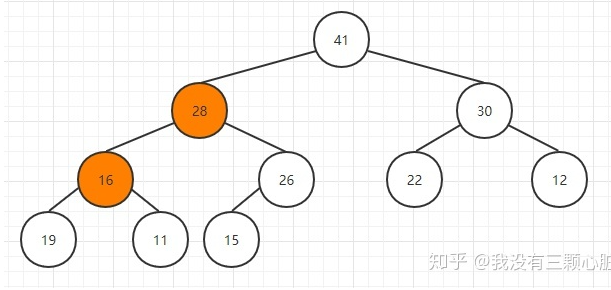
完成取出最大元素的操作：

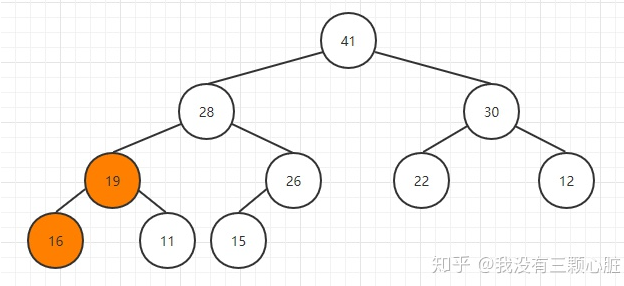
对应的代码如下：

// 看堆中的最大元素public E findMax(){
    if(data.getSize() == 0)
        throw new IllegalArgumentException("Can not findMax when heap is empty.");
    return data.get(0);
}
// 取出堆中最大元素public E extractMax(){

    E ret = findMax();

    data.swap(0, data.getSize() - 1);
    data.removeLast();
    siftDown(0);

    return ret;
}
private void siftDown(int k){

    while(leftChild(k) < data.getSize()){
        int j = leftChild(k); // 在此轮循环中,data[k]和data[j]交换位置        if( j + 1 < data.getSize() &&
                data.get(j + 1).compareTo(data.get(j)) > 0 )
            j ++;
        // data[j] 是 leftChild 和 rightChild 中的最大值
        if(data.get(k).compareTo(data.get(j)) >= 0 )
            break;

        data.swap(k, j);
        k = j;
    }
}

Replace 和 Heapify

Replace这个操作其实就是取出堆中最大的元素之后再新插入一个元素，常规的做法是取出最大元素之后，再利用上面的插入新元素的操作对堆进行Sift Up操作，但是这里有一个小技巧就是直接使用新元素替换掉堆顶元素，之后再进行Sift Down操作，这样就把两次O(logn）的操作变成了一次O(logn)：

// 取出堆中的最大元素，并且替换成元素epublic E replace(E e){

    E ret = findMax();
    data.set(0, e);
    siftDown(0);
    return ret;
}

Heapify翻译过来就是堆化的意思，就是将任意数组整理成堆的形状，通常的做法是遍历数组从0开始添加创建一个新的堆，但是这里存在一个小技巧就是把当前数组就看做是一个完全二叉树，然后从最后一个非叶子结点开始进行Sift Down操作就可以了，最后一个非叶子结点也很好找，就是最后一个结点的父亲结点，大家可以验证一下：

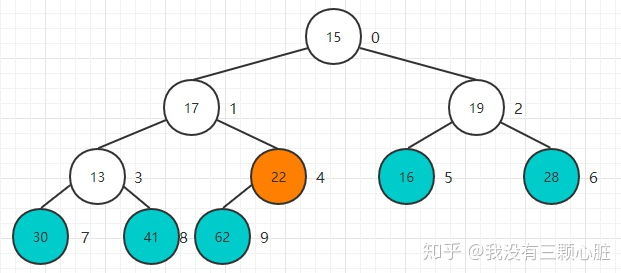
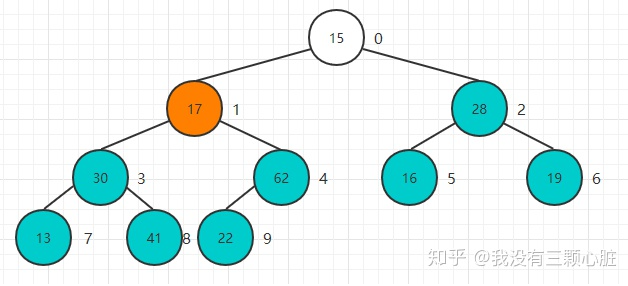
从22这个节点开始，依次开始Sift Down操作：

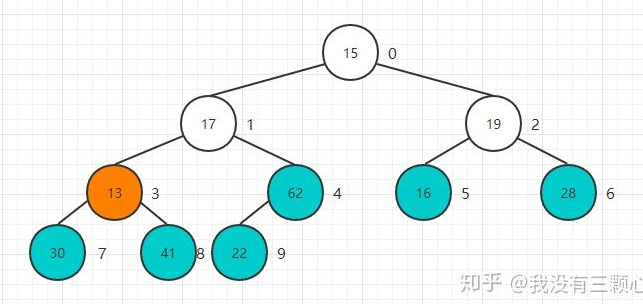
重复该过程直到堆顶元素：

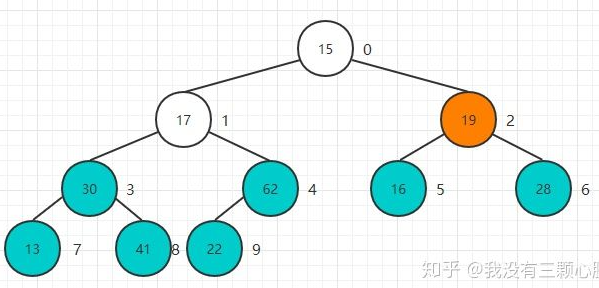
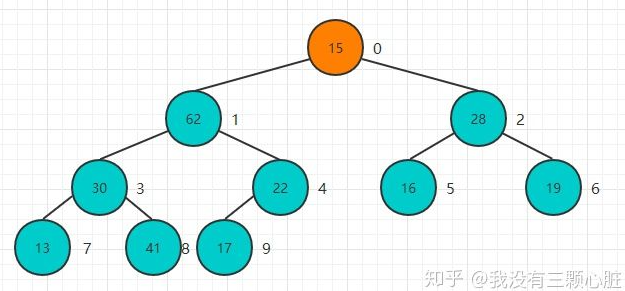
完成堆化操作：

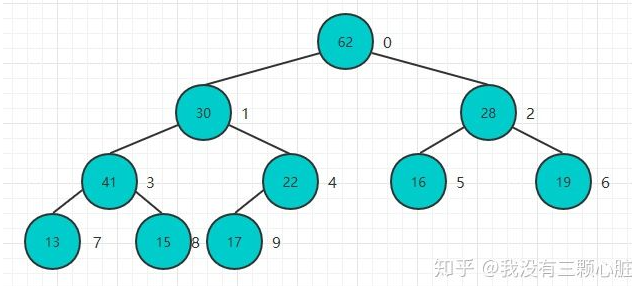
将n个元素逐个插入到一个空堆中，算法复杂度是O(nlogn)，而heapify的过程，算法复杂度为O(n)，这是有一个质的飞跃的，下面是代码：

public MaxHeap(E[] arr){
    data = new Array<>(arr);
    for(int i = parent(arr.length - 1) ; i >= 0 ; i --)
        siftDown(i);
}

基于堆的优先队列

首先我们的队列仍然需要继承我们之前将队列时候声明的哪个接口Queue，然后实现这个接口中的方法就可以了，子类简单写一下：

public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {

    private MaxHeap<E> maxHeap;

    public PriorityQueue(){ maxHeap = new MaxHeap<>(); }
    @Override    public int getSize(){ return maxHeap.size(); }
    @Override    public boolean isEmpty(){ return maxHeap.isEmpty(); }
    @Override    public E getFront(){ return maxHeap.findMax(); }
    @Override    public void enqueue(E e){ maxHeap.add(e); }
    @Override    public E dequeue(){ return maxHeap.extractMax(); }
}

Java中的PriorityQueue

在Java中也实现了自己的优先队列java.util.PriorityQueue，与我们自己写的不同之处在于，Java中内置的为最小堆，然后就是一些函数名不一样，底层还是维护了一个Object类型的数组，大家可以戳戳看有什么不同，另外如果想要把最小堆变成最大堆可以给PriorityQueue传入自己的比较器，例如：

// 默认为最小堆
PriorityQueue<Integer> pq = new PriorityQueue<>();

pq.add(5);
pq.add(2);
pq.add(1);
pq.add(10);
pq.add(3);
while (!pq.isEmpty()) {
    System.out.println(pq.poll() + ", ");
}
System.out.println();
System.out.println("————————————————————————");
// 使用Lambda表达式传入自己的比较器转换成最大堆PriorityQueue<Integer> pq2 = new PriorityQueue<>((a, b) -> b - a);
pq2.add(5);
pq2.add(2);
pq2.add(1);
pq2.add(10);
pq2.add(3);
while (!pq2.isEmpty()) {
    System.out.println(pq2.poll() + ", ");
}