树是一种“层次”关系,图是“网络”关系。
树和图的区别
| 树 | 图 |
|---|---|
| 树是一种特殊的图,它永远不会有多个路径。从A到B总是有一种方法。 | 图是一种具有多种方法来从任何点A到达任何其他点B的系统。 |
| 必须连接树。 | 可能未连接图形 |
| 由于它已连接,所以我们可以从一个特定结点到达所有其他结点。这种搜索称为遍历。 | 遍历可能不适用于图形。因为图形可能未连接。 |
| 树不包含回路,电路。 | 图可能包含自循环,循环。 |
| 树中必须有一个根节点。 | 图中没有这种根节点。 |
| 我们在树上遍历。这意味着从某个角度出发,我们进入树的每个节点。 | 我们在图上进行搜索。这意味着从任何节点开始尝试找到我们需要的特定结点。 |
| 树可以进行前序,中序,后序遍历。 | 图可以进行深度优先遍历和广度优先遍历。 |
| 树是有向无环图。 | 图是循环的或非循环的。 |
| 树是一个分层的模型结构。 | 图是网络模型。 |
| 所有的树都是图。 | 但是所有的图都不是树。 |
| 根据不同的属性,树可以分为二叉树,二叉搜索树,AVL树,堆。 | 图可以分为有向图和无向图。 |
| 如果树有n个顶点,则它必须仅有n-1条边。 | 在图中,变得数量不取决与顶点的数量。 |
| 与图形相比,复杂度更低。 | 由于循环,比树要复杂。 |
树的数据结构
树,和图一样也是一系列点的集合。
有一个根节点。这个根节点有一些子节点。
子节点也有它们自己的孙子节点。
不断重复直到所有的数据都被用树的数据结构表示。
下面的图表示了一个树的数据结构
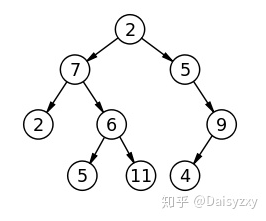
有向无环的图–树——-》并查集
树是没有环的图
图的数据结构
图从数学领域进化而来,
主要被用来描述一个从一个位置到另一个位置的路线的模型。
一个图包含一系列的点和一系列的边。
边用来把点连接起来。
路线是用来描述共用一条边的点的轨迹的术语。
这个图表示了一个三个点和三个边的图。
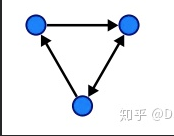
图最经典的实现是找两个点之间的路径。
找到从一个点到另一个点到最短路径,和找访问所有节点的最短路径。








