一致性哈希算法

Marlowe

发布于：May 29, 2021

2.9k words

10 min

一致性哈希算法在1997年由麻省理工学院的Karger等人在解决分布式Cache中提出的，设计目标是为了解决因特网中的热点(Hot spot)问题，初衷和CARP十分类似。一致性哈希修正了CARP使用的简单哈希算法带来的问题，使得DHT可以在P2P环境中真正得到应用。

简介

常见的负载均衡方法有很多，但是它们的优缺点也都很明显：

随机访问策略：系统随机访问，缺点：可能造成服务器负载压力不均衡，俗话讲就是撑的撑死，饿的饿死。
轮询策略：请求均匀分配，如果服务器有性能差异，则无法实现性能好的服务器能够多承担一部分。
权重轮询策略：权值需要静态配置，无法自动调节，不适合对长连接和命中率有要求的场景。
Hash取模策略：不稳定，如果列表中某台服务器宕机，则会导致路由算法产生变化，由此导致命中率的急剧下降。
一致性哈希策略。

以上几个策略，排除本篇介绍的一致性哈希，可能使用最多的就是 Hash取模策略了。Hash取模策略的缺点也是很明显的，这种缺点也许在负载均衡的时候不是很明显，但是在涉及数据访问的主从备份和分库分表中就体现明显了。

一致性Hash性质

考虑到分布式系统每个节点都有可能失效，并且新的节点很可能动态的增加进来，如何保证当系统的节点数目发生变化时仍然能够对外提供良好的服务，这是值得考虑的，尤其实在设计分布式缓存系统时，如果某台服务器失效，对于整个系统来说如果不采用合适的算法来保证一致性，那么缓存于系统中的所有数据都可能会失效（即由于系统节点数目变少，客户端在请求某一对象时需要重新计算其hash值（通常与系统中的节点数目有关），由于hash值已经改变，所以很可能找不到保存该对象的服务器节点），因此一致性hash就显得至关重要，良好的分布式cahce系统中的一致性hash算法应该满足以下几个方面：

平衡性(Balance)

平衡性是指哈希的结果能够尽可能分布到所有的缓冲中去，这样可以使得所有的缓冲空间都得到利用。很多哈希算法都能够满足这一条件。

单调性(Monotonicity)

单调性是指如果已经有一些内容通过哈希分派到了相应的缓冲中，又有新的缓冲区加入到系统中，那么哈希的结果应能够保证原有已分配的内容可以被映射到新的缓冲区中去，而不会被映射到旧的缓冲集合中的其他缓冲区。简单的哈希算法往往不能满足单调性的要求，如最简单的线性哈希：x = (ax + b) mod (P)，在上式中，P表示全部缓冲的大小。不难看出，当缓冲大小发生变化时(从P1到P2)，原来所有的哈希结果均会发生变化，从而不满足单调性的要求。哈希结果的变化意味着当缓冲空间发生变化时，所有的映射关系需要在系统内全部更新。而在P2P系统内，缓冲的变化等价于Peer加入或退出系统，这一情况在P2P系统中会频繁发生，因此会带来极大计算和传输负荷。单调性就是要求哈希算法能够应对这种情况。

分散性(Spread)

在分布式环境中，终端有可能看不到所有的缓冲，而是只能看到其中的一部分。当终端希望通过哈希过程将内容映射到缓冲上时，由于不同终端所见的缓冲范围有可能不同，从而导致哈希的结果不一致，最终的结果是相同的内容被不同的终端映射到不同的缓冲区中。这种情况显然是应该避免的，因为它导致相同内容被存储到不同缓冲中去，降低了系统存储的效率。分散性的定义就是上述情况发生的严重程度。好的哈希算法应能够尽量避免不一致的情况发生，也就是尽量降低分散性。

负载(Load)

负载问题实际上是从另一个角度看待分散性问题。既然不同的终端可能将相同的内容映射到不同的缓冲区中，那么对于一个特定的缓冲区而言，也可能被不同的用户映射为不同的内容。与分散性一样，这种情况也是应当避免的，因此好的哈希算法应能够尽量降低缓冲的负荷。

平滑性(Smoothness)

平滑性是指缓存服务器的数目平滑改变和缓存对象的平滑改变是一致的。

算法思想

一致性哈希算法通过一个叫作一致性哈希环的数据结构实现。这个环的起点是 0，终点是 2^32 - 1，并且起点与终点连接，故这个环的整数分布范围是 [0, 2^32-1]，如下图所示：

1 将对象放置到哈希环

假设我们有 “semlinker”、”kakuqo”、”lolo”、”fer” 四个对象，分别简写为 o1、o2、o3 和 o4，然后使用哈希函数计算这个对象的 hash 值，值的范围是 [0, 2^32-1]：

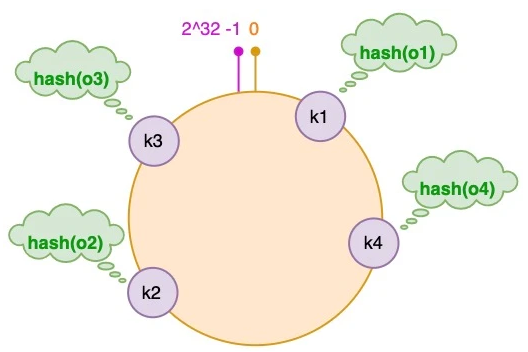
图中对象的映射关系如下：

1 2	hash(o1) = k1; hash(o2) = k2; hash(o3) = k3; hash(o4) = k4;

2 将服务器放置到哈希环

接着使用同样的哈希函数，我们将服务器也放置到哈希环上，可以选择服务器的 IP 或主机名作为键进行哈希，这样每台服务器就能确定其在哈希环上的位置。这里假设我们有 3 台缓存服务器，分别为 cs1、cs2 和 cs3：

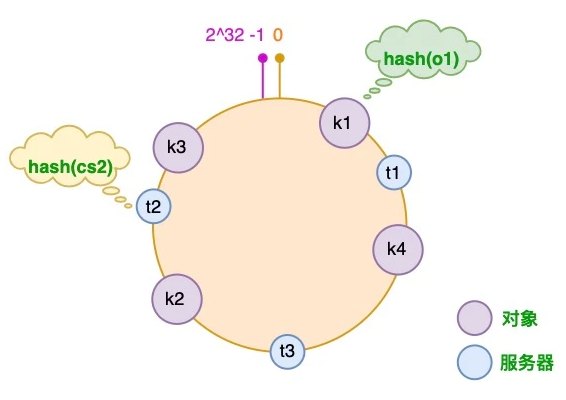
图中服务器的映射关系如下：

1	hash(cs1) = t1; hash(cs2) = t2; hash(cs3) = t3; # Cache Server

3 为对象选择服务器

将对象和服务器都放置到同一个哈希环后，在哈希环上顺时针查找距离这个对象的 hash 值最近的机器，即是这个对象所属的机器。 以 o2 对象为例，顺序针找到最近的机器是 cs2，故服务器 cs2 会缓存 o2 对象。而服务器 cs1 则缓存 o1，o3 对象，服务器 cs3 则缓存 o4 对象。

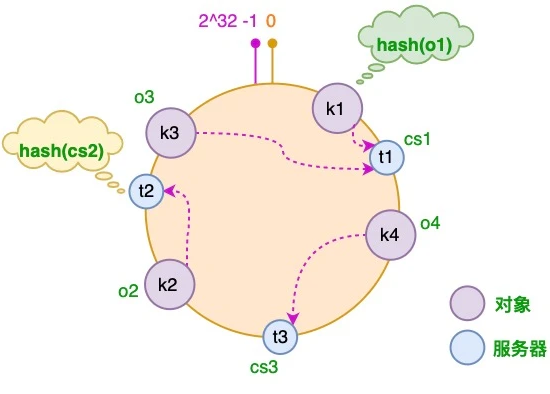
4 服务器增加的情况

假设由于业务需要，我们需要增加一台服务器 cs4，经过同样的 hash 运算，该服务器最终落于 t1 和 t2 服务器之间，具体如下图所示：

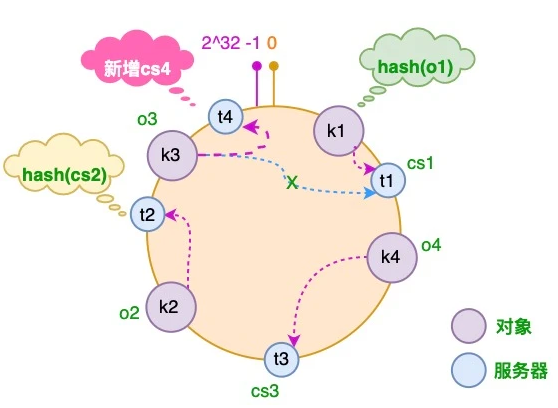
对于上述的情况，只有 t1 和 t2 服务器之间的对象需要重新分配。在以上示例中只有 o3 对象需要重新分配，即它被重新到 cs4 服务器。在前面我们已经分析过，如果使用简单的取模方法，当新添加服务器时可能会导致大部分缓存失效，而使用一致性哈希算法后，这种情况得到了较大的改善，因为只有少部分对象需要重新分配。

5 服务器减少的情况

假设 cs3 服务器出现故障导致服务下线，这时原本存储于 cs3 服务器的对象 o4，需要被重新分配至 cs2 服务器，其它对象仍存储在原有的机器上。

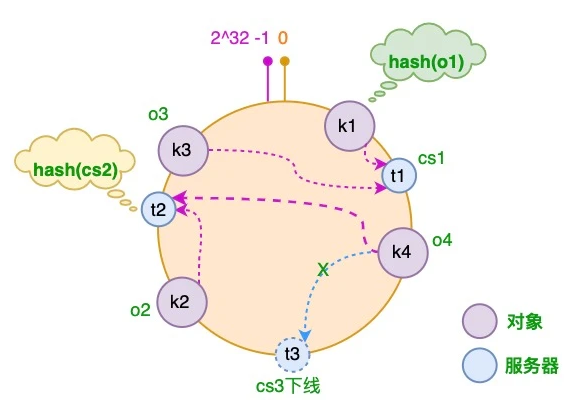
6 虚拟节点

到这里一致性哈希的基本原理已经介绍完了，但对于新增服务器的情况还存在一些问题。新增的服务器 cs4 只分担了 cs1 服务器的负载，服务器 cs2 和 cs3 并没有因为 cs4 服务器的加入而减少负载压力。如果 cs4 服务器的性能与原有服务器的性能一致甚至可能更高，那么这种结果并不是我们所期望的。

针对这个问题，我们可以通过引入虚拟节点来解决负载不均衡的问题。即将每台物理服务器虚拟为一组虚拟服务器，将虚拟服务器放置到哈希环上，如果要确定对象的服务器，需先确定对象的虚拟服务器，再由虚拟服务器确定物理服务器。

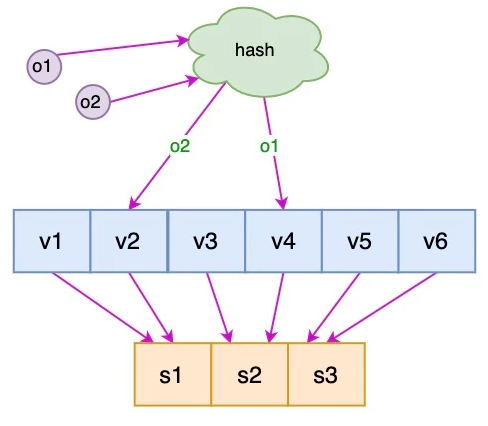
图中 o1 和 o2 表示对象，v1 ~ v6 表示虚拟服务器，s1 ~ s3 表示物理服务器。

一致性哈希算法实现

这里我们只介绍不带虚拟节点的一致性哈希算法实现：

import java.util.SortedMap;
import java.util.TreeMap;

public class ConsistentHashingWithoutVirtualNode {
    //待添加入Hash环的服务器列表
    private static String[] servers = {"192.168.0.1:8888", "192.168.0.2:8888", 
      "192.168.0.3:8888"};

    //key表示服务器的hash值，value表示服务器
    private static SortedMap<Integer, String> sortedMap = new TreeMap<Integer, String>();

    //程序初始化，将所有的服务器放入sortedMap中
    static {
        for (int i = 0; i < servers.length; i++) {
            int hash = getHash(servers[i]);
            System.out.println("[" + servers[i] + "]加入集合中, 其Hash值为" + hash);
            sortedMap.put(hash, servers[i]);
        }
    }

    //得到应当路由到的结点
    private static String getServer(String key) {
        //得到该key的hash值
        int hash = getHash(key);
        //得到大于该Hash值的所有Map
        SortedMap<Integer, String> subMap = sortedMap.tailMap(hash);
        if (subMap.isEmpty()) {
            //如果没有比该key的hash值大的，则从第一个node开始
            Integer i = sortedMap.firstKey();
            //返回对应的服务器
            return sortedMap.get(i);
        } else {
            //第一个Key就是顺时针过去离node最近的那个结点
            Integer i = subMap.firstKey();
            //返回对应的服务器
            return subMap.get(i);
        }
    }

    //使用FNV1_32_HASH算法计算服务器的Hash值
    private static int getHash(String str) {
        final int p = 16777619;
        int hash = (int) 2166136261L;
        for (int i = 0; i < str.length(); i++)
            hash = (hash ^ str.charAt(i)) * p;
        hash += hash << 13;
        hash ^= hash >> 7;
        hash += hash << 3;
        hash ^= hash >> 17;
        hash += hash << 5;

        // 如果算出来的值为负数则取其绝对值
        if (hash < 0)
            hash = Math.abs(hash);
        return hash;
    }

    public static void main(String[] args) {
        String[] keys = {"semlinker", "kakuqo", "fer"};
        for (int i = 0; i < keys.length; i++)
            System.out.println("[" + keys[i] + "]的hash值为" + getHash(keys[i])
                    + ", 被路由到结点[" + getServer(keys[i]) + "]");
    }

}

以上代码成功运行后，在控制台会输出以下结果：

[192.168.0.1:8888]加入集合中, 其Hash值为1326271016
[192.168.0.2:8888]加入集合中, 其Hash值为1132535844
[192.168.0.3:8888]加入集合中, 其Hash值为115798597

[semlinker]的hash值为1549041406, 被路由到结点[192.168.0.3:8888]
[kakuqo]的hash值为463104755, 被路由到结点[192.168.0.2:8888]
[fer]的hash值为1677150790, 被路由到结点[192.168.0.3:8888]