布隆过滤器

Marlowe

发布于：Apr 17, 2021

1.3k words

4 min

简介

布隆过滤器（Bloom Filter）是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多，缺点是有一定的误识别率和删除困难。

在讲述布隆过滤器的原理之前，我们先思考一个问题，如果想要判断一个元素是否存在，你通常会怎么做？一般的做法都是将其保存起来然后通过比较确认，一共会有如下几种情况：

如果使用线性表或者数组存储，则查找的时间复杂度为 O(n)。
如果使用树存储，则查找的时间复杂度为 O(logn)。
如果使用哈希表存储，则查找的时间复杂度为 O(log(n/m))，m 为哈希分桶数。

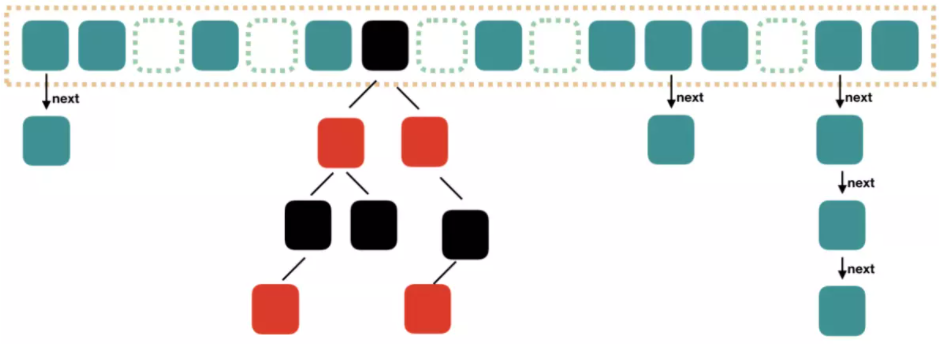
对于上述三种情况我相信大部分读者都倾向于哈希表，因为其时间复杂度最低（在极端情况下时间复杂度可以为 O(1) ），但是哈希表也有缺陷，例如存储容量占比高，考虑到负载因子的存在，通常存储空间都不会被用完。当然无论是哈希表、树、线性表，一旦元素的数量极多时，查询的速度会变得很慢，而且占用的空间也会大到无法想象。那么有办法解决没有呢？答案是有，布隆过滤器就是解决该问题的利器。

设计思想

布隆过滤器是一个由 一个长度为 M 比特的位数组（bit array）与 K 个哈希函数（hash function） 组成的数据结构。布隆过滤器主要用于用于检索一个元素是否在一个集合中。

位数组中的元素初始值都是 0 ，所有哈希函数可以把输入的数据均匀低散列。图例如下：

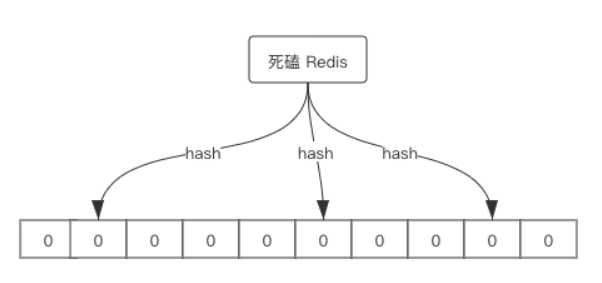
当要插入一个元素时，将其输入 K 个哈希函数，产生 K 个哈希值，同时以这些哈希值作为位数组的下标，将这些下标对应的比特值设置为 1。

当要查询一个元素时，同样是将其输入 K 个哈希函数，产生 K 个哈希值，然后检查这些哈希值中对应的比特值。如果有任意一个比特值为 0，则表明该元素一定不存在，如果所有比特值都是 1，则表明该元素可能存在，为什么不是一定存在呢？因为一个比特值为 1 有可能会受到其他元素的影响。所以 布隆过滤器是用于检测一个元素是否一定不存在或者有可能存在。

加入我们有一个布隆过滤器长度为 10，有 3 个哈希函数。这时我们我们将 ”死“插入到布隆过滤器中，经过三个哈希函数得到的哈希值为 3、6、9，则如下：

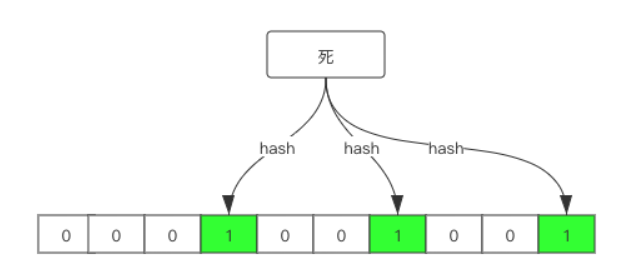
现在我们再存一个值：”磕“，假设得到的哈希值为 1 6 8，如下：

我们再查下 ”Redis“，假设返回的哈希值为 1 5 7，得到的比特值为 1 0 0 ，所以我们可以很确切地说”Redis“这个值一定不存在，如果查询 “Java” 得到的哈希值为 1 6 9，比特值为 1 1 1，那么我们是否可以说一定存在呢？答案是不可以，只能说 “Java” 这个值有可能存在。因为随着数据的增多，越来越多位置的比特值被设置为 1，有可能存在某个值从来没有被存储，但是哈希函数返回的位值都为 1 。

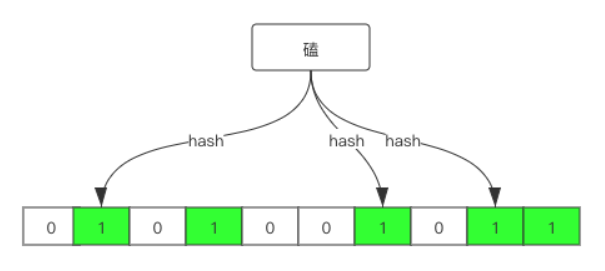
优缺点

优点

不需要存储数据，只用比特表示，因此在空间占用率上有巨大的优势
检索效率高，插入和查询的时间复杂度都为 O(K)（K 表示哈希函数的个数）
哈希函数之间相互独立，可以在硬件指令层次并行计算，因此效率较高。

缺点

存在不确定的因素，无法判断一个元素是否一定存在，所以不适合要求 100% 准确率的场景
只能插入和查询元素，不能删除元素。

实例

关于布隆过滤器，我们不需要自己实现，Guava 已经帮助我们实现了，使用起来非常简单。

引入 pom

<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId>
    <version>25.1-jre</version>
</dependency>

使用

public static void main(String... args){
        /**
         * 创建一个插入对象为一亿，误报率为0.01%的布隆过滤器
         */
        BloomFilter<CharSequence> bloomFilter = BloomFilter.create(Funnels.stringFunnel(Charset.forName("utf-8")), 100000000, 0.0001);
        bloomFilter.put("死");
        bloomFilter.put("磕");
        bloomFilter.put("Redis");

        System.out.println(bloomFilter.mightContain("Redis"));
        System.out.println(bloomFilter.mightContain("Java"));
    }