B树
简介
- 一种二叉搜索树。
- 除根节点外的所有非叶节点至少含有(M/2(向上取整)-1)个关键字,每个节点最多有M-1个关键字,并且以升序排列。所以M阶B树的除根节点外的所有非叶节点的关键字取值区间为[M/2-1(向上取整),M-1]。
- 每个节点最多有M-1个关键字。
动图演示

B+树
简介
- 有n棵子树的非叶子结点中含有n个关键字(b树是n-1个),这些关键字不保存数据,只用来索引,所有数据都保存在叶子节点(b树是每个关键字都保存数据)。
- 所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接(叶子节点组成一个链表)。
- 所有的非叶子结点可以看成是索引部分,结点中仅含其子树中的最大(或最小)关键字。
- 通常在b+树上有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点。
- 同一个数字会在不同节点中重复出现,根节点的最大元素就是b+树的最大元素。
B树与B+树的区别
B树每个节点都存储数据,所有节点组成这棵树。B+树只有叶子节点存储数据(B+数中有两个头指针:一个指向根节点,另一个指向关键字最小的叶节点),叶子节点包含了这棵树的所有数据,所有的叶子结点使用链表相连,便于区间查找和遍历,所有非叶节点起到索引作用。
B树中叶节点包含的关键字和其他节点包含的关键字是不重复的,B+树的索引项只包含对应子树的最大关键字和指向该子树的指针,不含有该关键字对应记录的存储地址。
B树中每个节点(非根节点)关键字个数的范围为
[m/2(向上取整)-1,m-1](根节点为[1,m-1]),并且具有n个关键字的节点包含(n+1)棵子树。B+树中每个节点(非根节点)关键字个数的范围为[m/2(向上取整),m](根节点为[1,m]),具有n个关键字的节点包含(n)棵子树。B+树中查找,无论查找是否成功,每次都是一条从根节点到叶节点的路径。
B树的优点
B树的每一个节点都包含key和value,因此经常访问的元素可能离根节点更近,因此访问也更迅速。
B+树的优点
- 所有的叶子结点使用链表相连,便于区间查找和遍历。B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻,所以缓存命中性没有B+树好。
- b+树的中间节点不保存数据,能容纳更多节点元素。
B树和B+树的共同优点
考虑磁盘IO的影响,它相对于内存来说是很慢的。数据库索引是存储在磁盘上的,当数据量大时,就不能把整个索引全部加载到内存了,只能逐一加载每一个磁盘页(对应索引树的节点)。所以我们要减少IO次数,对于树来说,IO次数就是树的高度,而“矮胖”就是b树的特征之一,m的大小取决于磁盘页的大小。
B+树比B树好在哪里
B+树的磁盘读写代价更低
B+的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。B+树的数据信息遍历更加方便
B+树只要遍历叶子节点就可以实现整棵树的遍历,而B树不支持这样的操作(或者说效率太低),而且 在数据库中基于范围的查询是非常频繁的,所以数据库索引基本采用B+树。
- B+树的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
为什么 MySQL 的索引要使用 B+ 树而不是其它树形结构?
数据库访问数据要通过页,一个页就是一个B+树节点,访问一个节点相当于一次I/O操作,所以越快能找到节点,查找性能越好。
B+树的特点就是够矮够胖,能有效地减少访问节点次数从而提高性能。
下面,我们来对比一个二叉树、多叉树、B树和B+树。
二叉树
二叉树是一种二分查找树,有很好的查找性能,相当于二分查找。
但是当N比较大的时候,树的深度比较高。数据查询的时间主要依赖于磁盘IO的次数,二叉树深度越大,查找的次数越多,性能越差。
最坏的情况是退化成了链表,如下图:

为了让二叉树不至于退化成链表,人们发明了AVL树(平衡二叉搜索树):任何结点的左子树和右子树高度最多相差1。
多叉树
多叉树就是节点可以是M个,能有效地减少高度,高度变小后,节点变少I/O自然少,性能比二叉树好了。
B树
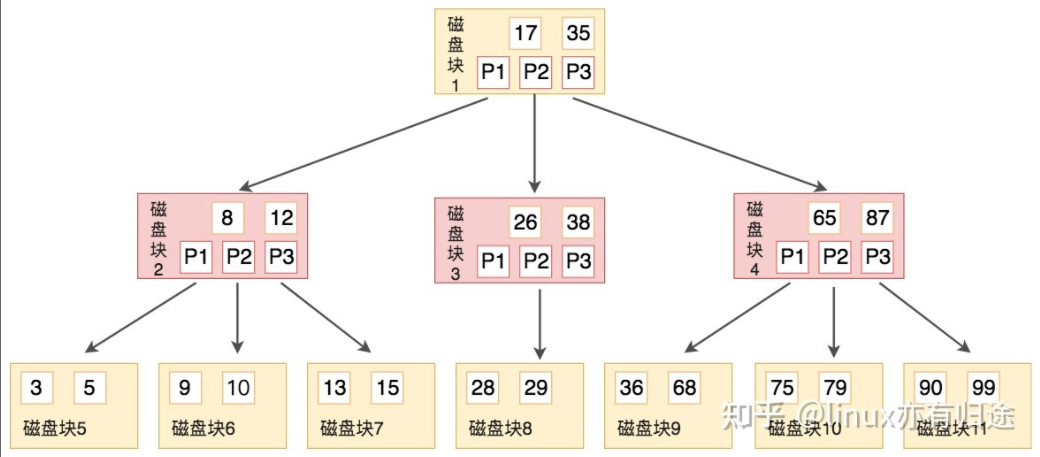
B树简单地说就是多叉树,每个叶子会存储数据,和指向下一个节点的指针。
例如要查找9,步骤如下
- 我们与根节点的关键字 (17,35)进行比较,9 小于 17 那么得到指针 P1;
- 按照指针 P1 找到磁盘块 2,关键字为(8,12),因为 9 在 8 和 12 之间,所以我们得到指针 P2;
- 按照指针 P2 找到磁盘块 6,关键字为(9,10),然后我们找到了关键字 9。
B+树
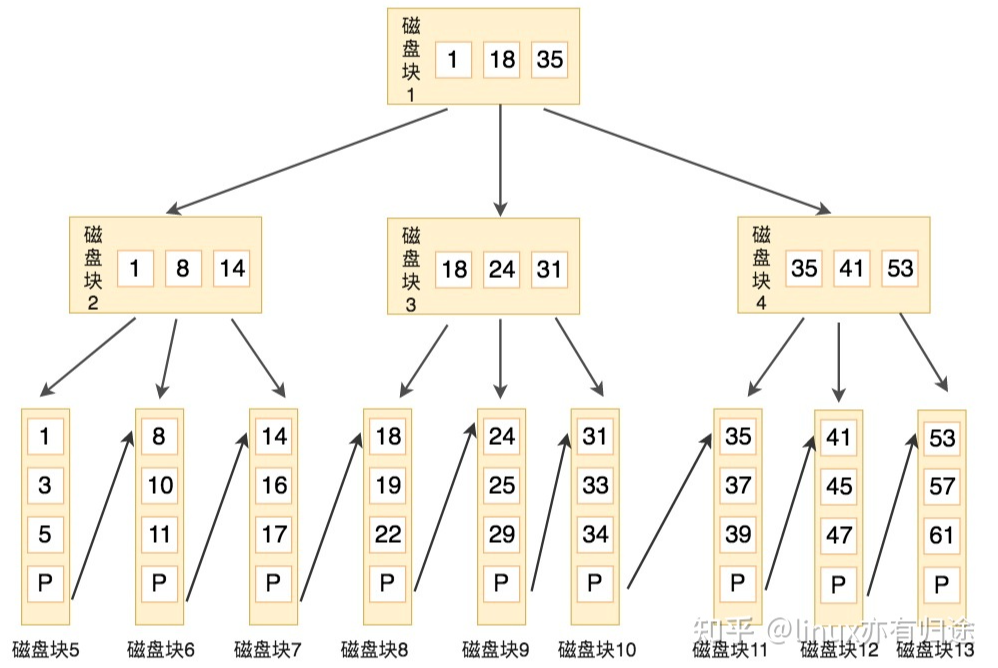
B+树是B树的改进,简单地说是:只有叶子节点才存数据,非叶子节点是存储的指针;所有叶子节点构成一个有序链表。
B+树的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小,如果把所有同一内部节点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多,一次性读入内存的需要查找的关键字也就越多,相对IO读写次数就降低了。
例如要查找关键字16,步骤如下:
与根节点的关键字 (1,18,35) 进行比较,16 在 1 和 18 之间,得到指针 P1(指向磁盘块 2)
找到磁盘块 2,关键字为(1,8,14),因为 16 大于 14,所以得到指针 P3(指向磁盘块 7)
找到磁盘块 7,关键字为(14,16,17),然后我们找到了关键字 16,所以可以找到关键字 16 所对应的数据。
B+树与B树的不同
- B+树非叶子节点不存在数据只存索引,B树非叶子节点存储数据。
- B+树查询效率更高。B+树使用双向链表串连所有叶子节点,区间查询效率更高(因为所有数据都在B+树的叶子节点,扫描数据库 只需扫一遍叶子结点就行了),但是B树则需要通过中序遍历才能完成查询范围的查找。
- B+树查询效率更稳定。B+树每次都必须查询到叶子节点才能找到数据,而B树查询的数据可能不在叶子节点,也可能在,这样就会造成查询的效率的不稳定。
- B+树的磁盘读写代价更小。B+树的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小,通常B+树矮更胖,高度小查询产生的I/O更少。
为什么用B+树做索引而不用红黑树?
AVL 树(平衡二叉树)和红黑树(二叉查找树)基本都是存储在内存中才会使用的数据结构。在大规模数据存储的时候,红黑树往往出现由于树的深度过大而造成磁盘IO读写过于频繁,进而导致效率低下的情况。为什么会出现这样的情况,要获取磁盘上数据,必须先通过磁盘移动臂移动到数据所在的柱面,然后找到指定盘面,接着旋转盘面找到数据所在的磁道,最后对数据进行读写。磁盘IO代价主要花费在查找所需的柱面上,树的深度过大会造成磁盘IO频繁读写。根据磁盘查找存取的次数往往由树的高度所决定,所以,只要我们通过某种较好的树结构减少树的结构尽量减少树的高度,B+树可以有多个子女,从几十到上千,可以降低树的高度。
数据库系统的设计者巧妙利用了磁盘预读原理,将一个节点的大小设为等于一个页,这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的,在实际实现B-Tree还需要使用如下技巧:每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上也存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了一个node只需一次I/O。
一些问题
MySQL中存储索引用到的数据结构是B+树,B+树的查询时间跟树的高度有关,是log(n),如果用hash存储,那么查询时间是O(1)。既然hash比B+树更快,为什么mysql用B+树来存储索引呢?
一、从内存角度上说,数据库中的索引一般时在磁盘上,数据量大的情况可能无法一次性装入内存,B+树的设计可以允许数据分批加载。
二、从业务场景上说,如果只选择一个数据那确实是hash更快,但是数据库中经常会选中多条这时候由于B+树索引有序,并且又有链表相连,它的查询效率比hash就快很多了。








