常用排序算法Java实现

Marlowe
算法

发布于：Mar 20, 2021
次浏览

3.3k words

14 min

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。

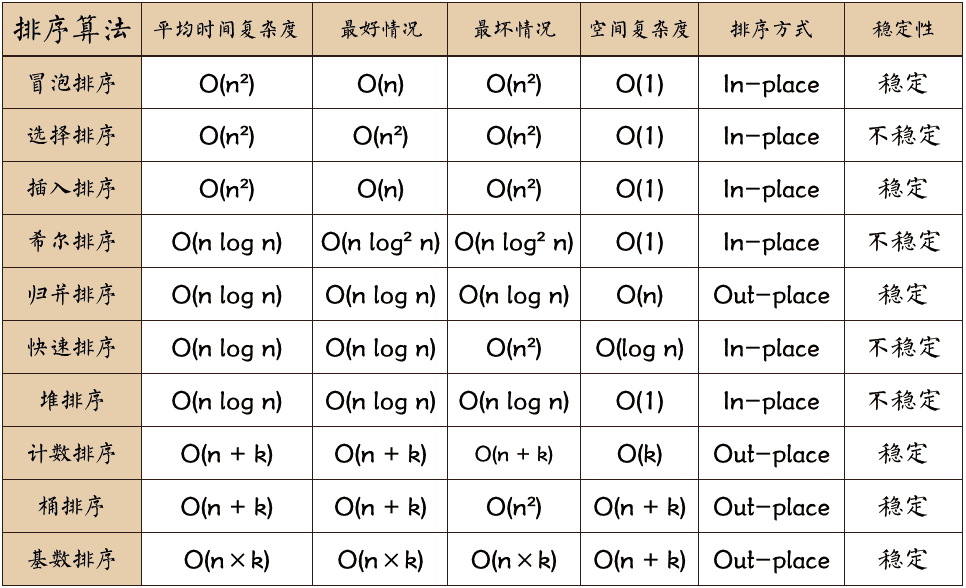
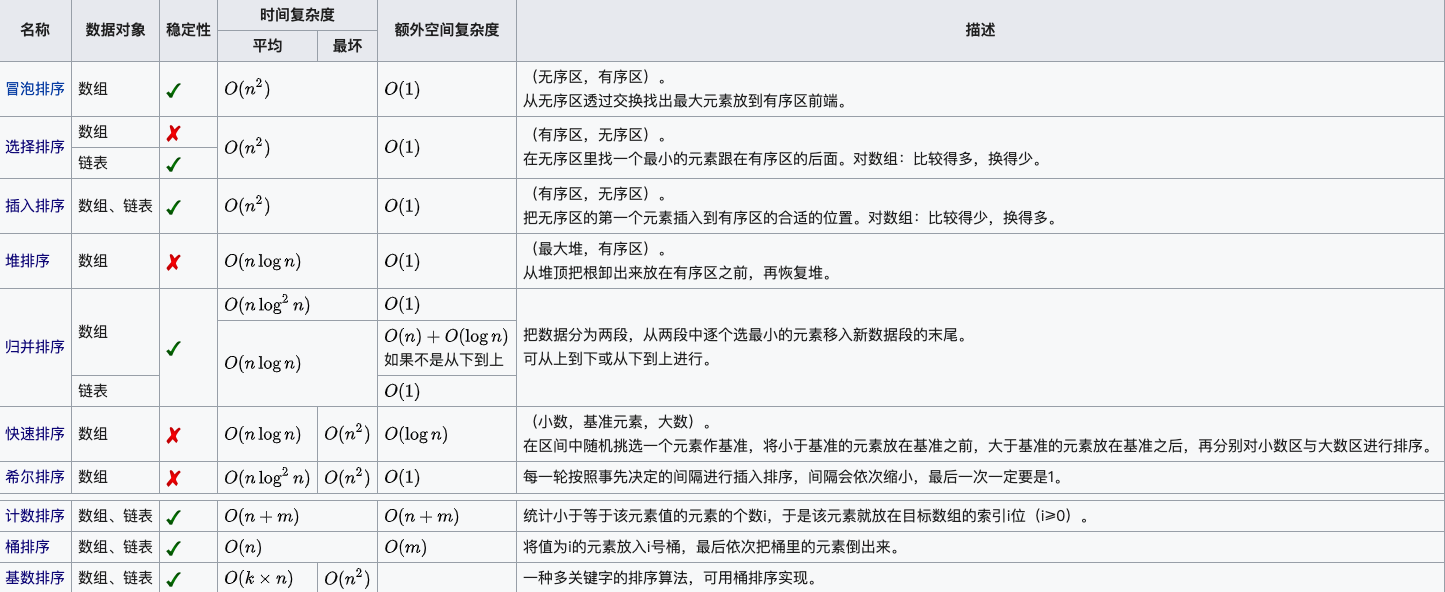
算法概览

20210320151556

20210320151637

排序算法

1 冒泡排序

算法思想
从左到右不断交换相邻逆序的元素，在一轮的循环之后，可以让未排序的最大元素上浮到右侧。
在一轮循环中，如果没有发生交换，那么说明数组已经是有序的，此时可以直接退出。
动图演示
冒泡排序
最好情况
当输入的数据已经是正序
最差情况
当输入的数据是反序
代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * 冒泡排序
 *
 * @param nums
 */
public static void bubbleSort(int[] nums) {
    int n = nums.length;
    boolean flag = false;
    for (int i = 0; i < n - 1 && !flag; i++) {
        flag = true;
        for (int j = 0; j < n - 1 - i; j++) {
            // 如果全都排好，则flag = true,跳出循环
            if (nums[j] > nums[j + 1]) {
                flag = false;
                swap(nums, j, j + 1);
            }
        }
    }
    System.out.println(Arrays.toString(nums));
}

2 选择排序

算法思想
每一次从未排序的集合中选出最小的数，依次放在第1、2、3…位置处
动图演示
选择排序

最好情况
当输入的数据已经是正序
最差情况
当输入的数据是反序

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * 选择排序
 *
 * @param nums
 */
public static void selectSort(int[] nums) {
    int n = nums.length;
    // 比较n - 1 轮
    for (int i = 0; i < n - 1; i++) {
        int min = i;
        // 每一轮找到最小值的下标
        for (int j = i + 1; j < n; j++) {
            if (nums[j] < nums[min]) {
                min = j;
            }
        }
        // 找到最小值与当前值交换
        if (min != i) {
            swap(nums, i, min);
        }
    }
    System.out.println(Arrays.toString(nums));
}

3 插入排序

算法思想
将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

动图演示

插入排序

最好情况
如果序列是完全有序的，插入排序只要比较n次，无需移动，时间复杂度为O(N)
最差情况
如果序列是逆序的，插入排序要比较O（N2）和移动O(N2)
代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * 插入排序
 * @param nums
 */
public static void insertSort(int[] nums) {
    int n = nums.length;
    for (int i = 1; i < n; i++) {
        // 从后往前找，如果当前元素比最后一个元素都大，则当前轮次排序结束
        for (int j = i; j > 0 && nums[j] < nums[j - 1]; j--) {
            swap(nums, j, j - 1);
        }
    }
    System.out.println(Arrays.toString(nums));
}

4 希尔排序

算法思想
希尔排序是将待排序的数组元素 按下标的一定增量分组 ，分成多个子序列，然后对各个子序列进行直接插入排序算法排序；然后依次缩减增量再进行排序，直到增量为1时，进行最后一次直接插入排序，排序结束。
动图演示
希尔排序
最好情况
序列是正序排列，在这种情况下，需要进行的比较操作需（n-1）次。后移赋值操作为0次。即O(n)
最差情况
O(nlog2n)
代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * 希尔排序
 *
 * @param nums
 */
public static void shellSort(int[] nums) {
    int n = nums.length;
    // gap： 增量，每次减半
    for (int gap = n / 2; gap > 0; gap /= 2) {
        // i:代表即将插入的元素角标，作为每一组比较数据的最后一个元素角标
        for (int i = gap; i < n; i++) {
            // j:代表与i同一组的数组元素角标
            for (int j = i - gap; j >= 0; j -= gap) {
                if (nums[j] > nums[j + gap]) {
                    swap(nums, j, j + gap);
                }
            }
        }
    }
    System.out.println(Arrays.toString(nums));
}

5 归并排序

算法思想
归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
算法步骤：

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  4. 重复步骤 3 直到某一指针达到序列尾；
  5. 将另一序列剩下的所有元素直接复制到合并序列尾。

动图演示
归并排序
最好情况
O(nlogn)
最差情况
O(nlogn)
代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * 合并两个有序子数组
 * @param nums
 * @param low
 * @param mid
 * @param high
 * @param tmp
 */
public static void merge(int[] nums, int low, int mid, int high, int[] tmp) {
    int i = 0;
    int j = low;
    int k = mid + 1;
    while (j <= mid && k <= high) {
        if (nums[j] < nums[k]) {
            tmp[i++] = nums[j++];
        } else {
            tmp[i++] = nums[k++];
        }
    }
    while (j <= mid) {
        tmp[i++] = nums[j++];
    }
    while (k <= high) {
        tmp[i++] = nums[k++];
    }
    for (int l = 0; l < i; l++) {
        nums[low + l] = tmp[l];
    }
}

/**
 * 左右子数组分别递归分
 * @param nums
 * @param low
 * @param high
 * @param tmp
 */
public static void mergeSort(int[] nums, int low, int high, int[] tmp) {
    if (low < high) {
        int mid = (low + high) >> 1;
        mergeSort(nums, low, mid, tmp);
        mergeSort(nums, mid + 1, high, tmp);
        merge(nums, low, mid, high, tmp);
    }
}

6 快速排序

算法思想
快速排序通过一个切分元素将数组分为两个子数组，左子数组小于等于切分元素，右子数组大于等于切分元素，将这两个子数组排序也就将整个数组排序了。
算法步骤：

  1. 从数列中挑出一个元素，称为 “基准”（pivot）;
  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

动图演示
快速排序
最好情况
最好情况，递归树的深度为log2n，其空间复杂度也就为O(logn)
最差情况
最坏情况，需要进行n‐1递归调用，其空间复杂度为O(n^2)
代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * 快速排序
 *
 * @param nums
 * @param low
 * @param high
 */
public static void quickSort(int[] nums, int low, int high) {
    int i, j, tmp;
    if (low > high) {
        return;
    }
    i = low;
    j = high;
    //tmp就是基准位
    tmp = nums[low];
    while (i < j) {
        //先看右边，依次往左递减
        while (tmp <= nums[j] && i < j) {
            j--;
        }
        //再看左边，依次往右递增
        while (tmp >= nums[i] && i < j) {
            i++;
        }
        //如果满足条件则交换
        if (i < j) {
            swap(nums, i, j);
        }
    }
    //最后将基准为与i和j相等位置的数字交换
    nums[low] = nums[i];
    nums[i] = tmp;
    //递归调用左半数组
    quickSort(nums, low, j - 1);
    //递归调用右半数组
    quickSort(nums, j + 1, high);
}

7 堆排序

算法思想
堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

  1. 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
  2. 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

动图演示
堆排序
最好情况
O(nlogn)
最差情况
O(nlogn)
代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
public class HeapSort {
    public static void main(String[] args) {
        int arr[] = {88, 11, 22, 3, 5, 1, 19};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void sort(int[] arr) {
        int len = arr.length;
        buildHeap(arr, len);
        for (int i = len - 1; i > 0; i--) {
            //首尾交换
            swap(arr, 0, i);
            //重新维护堆性质
            heapify(arr, 0, --len);
        }
    }

    private static void buildHeap(int[] arr, int len) {
        for (int i = 0; i < len / 2; i++) {
            heapify(arr, i, len);
        }
    }

    private static void heapify(int[] arr, int index, int len) {
        int left = 2 * index + 1;
        int right = 2 * index + 2;
        int max = index;
        if (left < len && arr[left] > arr[max]) {
            max = left;
        }
        if (right < len && arr[right] > arr[max]) {
            max = right;
        }
        if (max != index) {
            swap(arr, max, index);
            heapify(arr, max, len);
        }
    }

    /**
     * 交换
     *
     * @param arr   数组
     * @param self  自身
     * @param other 另一个
     */
    private static void swap(int[] arr, int self, int other) {
        int tmp = arr[self];
        arr[self] = arr[other];
        arr[other] = tmp;
    }
}

8 计数排序

算法思想
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

算法的步骤如下：

  1. 找出待排序的数组中最大和最小的元素
  2. 统计数组中每个值为i的元素出现的次数，存入数组C的第i项
  3. 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
  4. 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

动图演示
计数排序

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 计数排序
 *
 * @param nums
 */
public static void countSort(int[] nums) {
    int max = Integer.MIN_VALUE;
    // 找到最大值
    for (int num : nums) {
        if (num > max) {
            max = num;
        }
    }
    int[] bucket = new int[max + 1];
    // 统计每个元素的个数
    for (int num : nums) {
        bucket[num]++;
    }
    int index = 0;
    for (int i = 0; i < bucket.length; i++) {
        while (bucket[i] > 0) {
            nums[index++] = i;
            bucket[i]--;
        }
    }
}

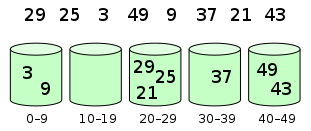
9 桶排序

算法思想
桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

  1. 在额外空间充足的情况下，尽量增大桶的数量
  2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

动图演示
元素分布在桶中：
桶排序
然后，元素在每个桶中排序：
桶排序

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public class BucketSort {
    public static void main(String[] args) {
        int arr[] = {5, 11, 7, 9, 2, 3, 12, 8, 6, 1, 4, 10};
        sort(arr, 5);
        System.out.println(Arrays.toString(arr));
    }


    private static void sort(int[] arr, int bucketSize) {
        if (arr.length == 0) {
            return;
        }
        int minValue = arr[0];
        int maxValue = arr[0];
        for (int value : arr) {
            if (value < minValue) {
                minValue = value;
            } else if (value > maxValue) {
                maxValue = value;
            }
        }
        int bucketCount = (maxValue - minValue) / bucketSize + 1;
        int[][] buckets = new int[bucketCount][0];
        // 利用映射函数将数据分配到各个桶中
        for (int item : arr) {
            int index = (item - minValue) / bucketSize;
            buckets[index] = arrAppend(buckets[index], item);
        }
        int arrIndex = 0;
        for (int[] bucket : buckets) {
            if (bucket.length <= 0) {
                continue;
            }
            // 对每个桶进行排序，这里使用了归并排序
            MergeSort.sort(bucket);
            for (int value : bucket) {
                arr[arrIndex++] = value;
            }
        }
    }

    /**
     * 自动扩容，并保存数据
     */
    private static int[] arrAppend(int[] arr, int value) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    }
}

10 基数排序

算法思想
基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

动图演示
基数排序

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/**
 * 基数排序
 * 考虑负数的情况还可以参考： https://code.i-harness.com/zh-CN/q/e98fa9
 */
public class RadixSort {

    public static void main(String[] args) {
        int arr[] = {5, 11, 7, 9, 2, 3, 12, 8, 6, 1, 4, 10};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static int[] sort(int[] arr) {
        int maxDigit = getMaxDigit(arr);
        return radixSort(arr, maxDigit);
    }

    /**
     * 获取最高位数
     */
    private static int getMaxDigit(int[] arr) {
        int maxValue = getMaxValue(arr);
        return getNumLength(maxValue);
    }

    private static int getMaxValue(int[] arr) {
        int maxValue = arr[0];
        for (int value : arr) {
            if (maxValue < value) {
                maxValue = value;
            }
        }
        return maxValue;
    }

    protected static int getNumLength(long num) {
        if (num == 0) {
            return 1;
        }
        int lenght = 0;
        for (long temp = num; temp != 0; temp /= 10) {
            lenght++;
        }
        return lenght;
    }

    private static int[] radixSort(int[] arr, int maxDigit) {
        int mod = 10;
        int dev = 1;

        for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
            // 考虑负数的情况，这里扩展一倍队列数，其中 [0-9]对应负数，[10-19]对应正数 (bucket + 10)
            int[][] counter = new int[mod * 2][0];

            for (int j = 0; j < arr.length; j++) {
                int bucket = ((arr[j] % mod) / dev) + mod;
                counter[bucket] = arrayAppend(counter[bucket], arr[j]);
            }

            int pos = 0;
            for (int[] bucket : counter) {
                for (int value : bucket) {
                    arr[pos++] = value;
                }
            }
        }

        return arr;
    }

    /**
     * 自动扩容，并保存数据
     *
     * @param arr
     * @param value
     */
    private static int[] arrayAppend(int[] arr, int value) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    }
}

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://xmmarlowe.github.io/2021/03/20/%E7%AE%97%E6%B3%95%E4%B8%8E%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84/%E5%B8%B8%E7%94%A8%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95Java%E5%AE%9E%E7%8E%B0/

Marlowe

更新于：Apr 15, 2021

评论